Расписание кружка

Вторник: 15.20-16.10

Четверг: 15.20-16.10

Суббота: 11.30-13.00, 08.10-10.00

Кабинет 21,субб. КГМТУ

Руководитель- Егорова С.Н.

Расписание кружка

Среда: 16.30-18.00

Четверг: 16.30-18.00

Суббота: 10.00-11.30

Кабинет 21,субб. КГМТУ

Руководитель- Куценко И.Л.

ГЛАВА 1. Обоснование принципа Дирихле.

1.1. Суть принципа Дирихле

Рассмотрим одну задачу:

В самолете летят 380 пассажиров. Докажите что по крайней мере двое из них родились в один и тот же день года.

Доказательство. Всего в году 365 или 366 дней, а пассажиров в самолете 380 – значит, их дни рождения не могут  приходиться на различные дни. Вообще если пассажиров больше, чем 366, то хотя бы у двоих дни рождения совпадают. А вот если пассажиров 366 не исключено, что все они родились в разные дни года, но это маловероятно (согласно теории вероятностей в случайно выбранной группе численностью свыше 22 человек совпадение дней рождения у некоторых из них более вероятно, нежели то, что у всех дни рождения приходятся на разные дни года.)

Логический  прием, использованный в приведенном доказательстве, называется принципом Дирихле – по имени Петера Густава Дирихле (1805-1895) немецкого математика, автора описанного метода.

Вот общая форма принципа Дирихле:

Если k∙n+1 предмет разложен в k ящиков, то, по крайней мере, в одном из ящиков лежит не меньше, чем n+1 предмет.

Докажем это  с помощью метода математической индукции. 

Доказательство.

1. Докажем правильность принципа при k=1. В этом случае всего будет k∙n+1=n+1 "предметов". Если их разложить в k=1 "ящиков", то в этом ящике будет n+1 "предмет".

2. Пусть при размещении p∙n+1 "предметов" в k=p "ящиков" найдется ящик, в котором не меньше, чем n+1 "предмет".

3. Докажем истинность этого и при k=p+1. В этом случае число "предметов" равно:

(p+1)·n+1 = (n·p+1) +N,

а число "ящиков" равно p+1.

Если в одном из этих "ящиков" больше, чем n "предметов", то есть не меньше, чем n+1 предмет, то утверждение доказано.

Если в этом "ящике" не больше, чем n "предметов", то в остальных p "ящиках" находятся не меньше, чем n·p+1 "предмет". А тогда, по предположению 2, найдется "ящик", в котором не меньше, чем n+1 "предмет".

Итак, в обоих случаях подтвердилось истинность утверждения для k=p+1. Принцип Дирихле доказан.

По традиции в популярной литературе принцип Дирихле объясняют на примере “зайцев” и “клеток’:

Если N зайцев сидят в n клетках и N>n, то хотя бы в одной клетке сидит более одного зайца.

1.2. П.Г.Л. Дирихле (биография).

Дирихле Петер Густав Лежен (13.02.1805 Дюрен – 5.05.1859 Гетенген), немецкий математик 1831-1855 гг. профессор Берлинского, с 1855 г. Гетенгенского университетов. Основал труды в области теории чисел и математического анализа. Дирихле доказал теорему о существовании бесконечно большого числа простых чисел во всякой арифметической прогрессии из целых чисел первый член и разность которой – числа взаимно простые. В области математического анализа Дирихле впервые точно сформулировал и исследовал понятие условной сходимости ряда, дал строгое доказательство возможности разложения в ряд Фурье функции, имеющей конечное число максимумов и минимумов. Работы Дирихле посвящены механике и математической физики.

ГЛАВА 2. Применение принципа Дирихле к решению

различных задач.

2.1. Логические задачи

Задача 1. В классе 30 человек. Саша Иванов в диктанте сделал 13 ошибок, а остальные – меньше. Докажите что по крайней мере 3 ученика сделали ошибок поровну (может быть по 0 ошибок.)

Доказательство. Здесь “зайцы” – ученики, “клетки” – число сделанных ошибок. В клетку 0 “посадим” всех, кто сделал ни одной ошибки, в клетку 1 – тех, у кого одна ошибка, в клетку 2 – две … и так до клетки 13, куда попал один Саша Иванов.

Теперь применим принцип Дирихле. Докажем утверждение задачи от противного. Предположим, никакие три ученика не сделали по одинаковому числу ошибок, то есть в каждую из “клеток”: 0, 1, 2, …, 12 попало меньше 3школьников. Тогда в каждой из них два человека или меньше, а всего в этих 13 клетках не более 2×13=26 человек. Добавив Сашу Иванова, все ровно не наберем 30 ребят. Противоречие. Значит, наше предположение неверно и, по крайней мере, трое учеников сделали поровну ошибок.

Задача 2. В Москве живет более 7,8 млн. жителей, на голове у каждого не более 100 тыс. волос. Докажите что в Москве есть по крайней мере 70 человек с одинаковым числом волос на голове.

Доказательство. Построим 100001 “клетку” для тех, у кого на голове нет волос вообще (0 волос), для тех, у кого на голове ровно 1 волос, ровно 2 волоса, …, ровно 100000 волос.

Распределим население города по “клеткам” (мысленно, разумеется). Если бы в каждой клетке находилось не более 70 человек, то всего в городе было бы не более 70×100001=700070 человек.

Таким образом, утверждение задачи можно усилить – есть, по крайней мере, 78 человек с одинаковым числом волос на голове.

Задача 3. На земле живет более 3,6 млрд. человек. Известно, что среди не более 1% людей старше 100 лет. Докажите, что найдется два человека, которые родились в одну и ту же секунду.

Доказательство. Оценим сначала число секунд за 100 лет. В соответствии с ныне действующим календарем за 100 лет бывает 24 високосных года и 76 простых лет (год, оканчивающийся на 00, считается простым.) Впрочем, для наших целей достаточно знать, что в каждом из них менее чем 370 дней. А за 100 лет пройдет меньше чем 37000 дней. В минуте 60 с; в часе 60 мин, значит, в часе 60×60=3600 с. В сутках 24 часа или 3600×24=86400 с. Значит, в сутках меньше 90000 с; а за 100 лет пройдет меньше 90000×37000=3330000000 с, то есть 3,33 млрд. с. Из условия следует, что не старше 100 лет, по крайней мере, 3,6×0,99=3,564 млрд. людей. Для завершения доказательства следует сослаться на принцип Дирихле.

Задача 4. Если класс из 30 человек рассадить в зале кинотеатра, то в любом случае хотя бы в одном ряду окажется не менее двух одноклассников. Если то же самое проделать с классом из 26 человек, то, по крайней мере, три ряда окажутся пустыми. Сколько рядов в зале?

Решение. Первое условие означает, что в зале не более 29 рядов. Действительно, если бы количество рядов было не меньше 30, то, очевидно, класс из 30 человек можно было бы рассадить не более чем по одному на каждый ряд.

     Второе условие означает, что количество рядов в зале не менее 29. Действительно, если количество рядов не больше 28, то, сажая учеников класса из 26 человек по очереди на пустые ряды, получим, что-либо в какой-то момент все ряды будут заняты, либо все 26 учеников будут сидеть по одному на 26 рядах, и в этом случае останутся свободными не более двух рядов.

Значит, в кинотеатре 29 рядов. Очевидно, что в этом случае оба условия задачи выполнены.

Задача 5. Петя написал на гранях кубика натуральные числа от 1 до 6. Вася кубика не видел, но утверждает, что:

а) у этого кубика есть две соседние грани, на которых написаны соседние числа;

б) таких пар соседних граней у кубика не меньше двух.

Прав ли он в обоих случаях? Почему?

Решение. В наборе натуральных чисел от 1 до 6 можно найти пять пар соседних чисел: 1 и 2, 2 и 3, 3 и 4, 4 и 5, 5 и 6. Каждая такая пара может быть написана либо на двух соседних гранях кубика, либо на двух противоположных. Но пар противоположных граней у кубика всего три. Поэтому их могут занимать не более трех пар соседних чисел. Значит, по крайней мере, две такие пары занимают соседние грани. Следовательно, можно утверждать, что Вася прав в обоих случаях.

Задача 6. В классе 25 человек. Известно, что среди любых трех из них есть двое друзей. Докажите, что есть ученик, у которого не меньше 12 друзей.

Доказательство. Рассмотрим двоих учеников класса, которые не дружат между собой. (Если таких учеников нет, то все ученики класса дружат между собой, значит, у каждого ученика имеются 24 друга, и задача решена.) Пусть этими двумя будут Вася и Петя. Тогда из оставшихся 23 учеников каждый дружит либо с Васей, либо с Петей. Действительно, если бы кто-то (скажем Коля) не дружил бы ни с Васей, ни с Петей, то мы имели бы троих учеников, среди которых не было бы друзей. Теперь если предположить, что и Вася, и Петя имеют не более 11 друзей, то всего в классе, кроме этих двоих было бы не больше 22 человек. Полученное противоречие показывает, что один из школьников имеет не менее 12 друзей.

Задача 7. Петя разрезал прямоугольный лист бумаги по прямой. Затем он разрезал по прямой один из получившихся кусков. Затем он проделал то же самое с одним из трех получившихся кусков и так далее. Докажите, что после достаточного количества разрезаний можно будет выбрать среди получившихся кусков 100 многоугольников с одинаковым числом вершин.

Доказательство. Обозначим через S_n суммарное количество сторон всех получившихся многоугольников после (n - 1)-го разделения (общее количество многоугольников при этом будет n). Докажем, что после 297 разрезов у Пети будет либо не меньше 100 треугольников, либо не меньше 100 четырехугольников. Предположим противное, тогда можно получить оценку снизу S₂₉₈≥99×3+99×4+100×5=298×4+1, поскольку среди 298 многоугольников не более 99 треугольников, не более 99 четырехугольников, а остальные многоугольники содержат не менее 5 сторон. С другой стороны, при каждом разрезании количество сторон увеличивается не более чем на 4, поэтому S_n≤298×4. Полученное противоречие доказывает утверждение.

Задача 8. Какое наибольшее число королей можно расставить  на шахматной доске так, чтобы они не били друг друга.

Доказательство. На шахматной доске можно расположить 16 королей, как показано на рис. 1.

Докажем, что расположение большего числа королей невозможно. Для этого предположим, что на доске можно разместить хотя бы 17 королей. Разобьем доску на 16 равных квадратов, как показано на рисунке 2. 

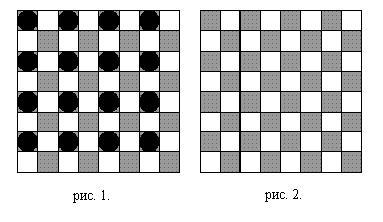
Примем эти квадраты за “ящики”, а все королей -  за “предметы”. По принципу Дирихле, найдется “ящик” с двумя “предметами”, то есть найдется квадрат, на полях которого стоят два короля. Очевидно, что на одном квадрате нельзя разместить двух королей так, чтобы они не били друг друга.

Получим противоречие, значит, наше предположение неверно, и на доске можно разместить не более 16 королей.

Ответ: 16 королей.

Задача 9. Восемь футбольных команд провели турнир, (каждая сыграла с каждой один раз). При этом не было "ничьих". Докажите, что можно выделить такие четыре команды A, B, C, D. что A выиграла у B, C и D; B выиграла у C и D; C выиграла у D.

Доказательство. Так как, по условию, в турнире не было "ничьих", то каждый из матчей (их было C₈²==28) заканчивался чьей-либо победой. Распределим все k×n+1=28 побед между восемью командами, приняв их за "предметы", а k=8 команд – за "ящики".

По принципу Дирихле, найдется “ящик” в котором не меньше, чем n+1=3+1=4 “предмета”. Иначе говоря, среди восьми команд найдутся хотя бы одна команда A, которая выиграла у четырех других команд, то есть имеет не менее четырех побед. Эти четыре команды между собой провели C₄²==6 матчей, то есть было 6 побед. Приняв 4 команды за “ящики”, а 6 побед за “предметы”, по принципу Дирихле получим, что найдется команда B, одержавшая, по меньшей мере, 2 победы над двумя командами C и D из четырех рассматриваемых.

Пусть в матче между командами C и D победила C. Тогда получим:

A победила B, C и D.

B победила C и D.

 C победила D.

Итак, мы нашли четыре команды A, B, C, D, удовлетворяющие условию задачи.

Задача 10. Выберем n человек. Докажите, что, по крайней мере, двое из них имеют одинаковое число знакомых среди выбранных.

Доказательство. Возможное число знакомых у каждого: 1, 2, 3,…, n-1. Возьмем n “ящиков”. Всех людей примем за “предметы”. Пусть номер  каждого “ящика” соответствует числу знакомых у людей – “предметов”, содержащихся в них.

     Рассмотрим два случая.

а) Людей, не имеющих ни одного знакомого, нет. В этом случае “ящик” N 0 – пуст. Тогда расположим n человек в остальных n-1 “ящиках”.

По принципу Дирихле, найдется “ящик”, в котором не менее двух “предметов”, то есть не менее двух человек будут иметь одинаковое количество знакомых.

Итак, в обоих случаях найдутся два человека с одинаковым числом знакомых. Значит, это справедливо и для общего случая.

Задача 11. Докажите, что среди 82 кубиков, каждый из которых выкрашен в определенный цвет, всегда можно выбрать 10 кубиков таких, что-либо все они выкрашены в разные цвета, либо все одного цвета.

Доказательство. 1. Примем за “ящики” возможные цвета кубиков, а за “предметы” – сами эти кубики.

Разложим кубики – “предметы” по “ящикам”. Так, чтобы в одном “ящике” лежали кубики одного цвета, а в разных – разного.

2. Рассмотрим два случая.

а) Если “ящиков” с кубиками больше 9 (не меньше 10), взяв по одному кубику из каждого “ящика”, получим не меньше 10 кубиков разного цвета.

б) Если “ящиков” с кубиками не больше 9, то разложим в эти “ящики” 82 кубика – “предмета”. По принципу Дирихле, в самом наихудшем варианте (когда “ящиков” 9) найдется “ящик”, в котором не меньше чем n+1=9+1=10 кубиков, одинакового окрашенных. Итак, в обоих случаях найдутся 10 кубиков, удовлетворяющих  условию задачи.

В следующих задачах на принцип Дирихле используется информация о том, что в некоторых “ящиках” число “предметов” можно заранее ограничить подходящей константой.

Задача 12. Восемь целых чисел подчинены условию:

0< a₁ < a₂ < a_{3 …} < a₈ < 16.

Докажите, что всегда существует такое число k, что из данных восьми чисел можно выбрать не менее трех, связанных соотношением: а_i − а_j = k.

Доказательство. 1. Из условия видно, что числа а₁, а₂, …, а₈ могут быть равными 1, 2, 3, …, 15. Тогда возможные разности двух чисел а_i и а_j: 1, 2, 3, …, 14. причем ясно, что разность 14 может быть получена лишь одним способом (15-1=14).

2. Примем за “ящики” возможные разности чисел (их 14). Пусть номер каждого “ящика” соответствует значению разности пар чисел, содержащихся в нем. “Предметы” – все пары чисел из а₁; a₂; a₃; …; a₈. Их 28 C₈²=. Разложим “предметы” в “ящики”.

С учетом, что в “ящике” N 14 не более одного “предмета”. Значит, на остальные k=13 “ящиков” приходится не менее k×n=27 “предметов” – пар чисел. Следовательно, по принципу Дирихле, из этих 13 “ящиков” найдется, по крайней мере, один “ящик”, содержащий не менее трех “предметов” (n=2; n+1=3). Номер этого “ящика” соответствует числу k, так как этот номер – значение разности чисел а_i и а_j (их три пары), находящихся в этом “ящике”.

3. Итак, мы доказали, что найдется число k такое, что из чисел а₁; …;а₈ найдутся не менее трех пар, связанных соотношением: а_i − а_j = k.

Задача 13. По краю круглого стола равномерно расставлены таблички с фамилиями дипломатов, участвующих в совещании. После начала совещания оказалось, что ни один из дипломатов не сидит против своей таблички. Можно ли повернуть стол так, чтобы, по крайней мере, два дипломата сидели против своих табличек?

Решение. 1. Пусть за столом сидят n дипломатов. Рассмотрим возможные положения стола по отношению к дипломатам. Число этих положений, очевидно, равно n. Примем их за “ящики”.

2. За “предметы” примем дипломатов, каждому из которых удовлетворяет лишь одно положение стола. Всего “предметов” n. Разместим “предметы” в “ящики”. С учетом, что в одном из положений – “ящиков” нет ни одного “предмета” (то есть, нет ни одного дипломата, которому удовлетворяет начальное положение стола). Следовательно, на остальные n-1 “ящиков” приходится n “предметов”. Отсюда, по принципу Дирихле, найдется “ящик”, в котором не менее двух “предметов”, то есть найдется положение стола, удовлетворяющее не менее чем двум дипломатам. Значит, можно повернуть стол так, чтобы два дипломата оказались напротив своих табличек.

Задача 14. Даны n+1 натуральных различных чисел, меньших 2n. Докажите, что из них можно выбрать три такие числа, что одно из них равна сумме двух других.

Доказательство. Рассмотрим наибольшее из n+1 выбранных чисел. По условию, оно меньше, чем 2n. Рассмотрим “наихудший” вариант, когда это число принимает наибольшее значение, то есть равно 2n−1. Все предыдущие 2n−2 чисел ряда разобьем на n−1 “ящиков” следующим образом:

Сумма чисел в каждом “ящике” равна 2n-1, то есть, равна наибольшему из n+1 выбр. чисел.

Выберем из n-1 “ящиков” оставшиеся n чисел (одно мы уже выбрали – наибольшее). По принципу Дирихле, найдется “ящик”, из которого мы взяли оба числа. Сумма этих чисел равна наибольшему числу 2n-1. Итак, нашлись три числа, сумма двух из которых равна третьему.

Во всех остальных вариантах (то есть, когда наибольшее из n+1 чисел меньше, чем 2n+1) “ящиков” будет меньше, чем n-1, а “предметов” – по-прежнему n. Значит, в этом случае тем более найдутся два числа, сумма которых равна третьему – наибольшему числу.

Задача 15. На шахматной доске расставлены числа от 1 до 64. Докажите, что при любой их расстановке найдутся две соседние клетки (имеющие общую сторону) такие, что разность между стоящими в них числами будет больше 4.

Доказательство. Поместим числа от 1 и 64 в противоположные клетки диагонали. Их соединяет линия, проходящая через 15 попарно соседних клеток, то есть содержащая 14 переходов. Допустим, что на каждом переходе приращение не превышает 4. Тогда общее не превышает 4×14=56<63. Но это противоречит условию, значит наше допущение не верно.

Задача 16. 106 т строительных материалов упаковано в ящиках; масса каждого не превышает 6 т. Грузовой лифт перевозит их на крышу небоскреба. Если масса груза более 25 т, лифт автоматически отключается. Какое количество рейсов лифта достаточно для перевозки груза?

Решение. В каждый из рейсов можно загрузить не менее 19 т. Поэтому достаточно 106:19, то есть 6 рейсов. 5 рейсов может оказаться недостаточно. Например, если 21 одинаковый ящик попытаться перевезти в 5 рейсов, то в одном из рейсов 5 ящиков общей массой 106×5/21>5 т.

Задача 17. Требуется доказать, что существует хотя бы одно иррациональное число – такое действительное число, которое нельзя представить в виде отношения m/n, двух натуральных чисел.

Доказательство. Такое число – это . В самом деле, по теореме Пифагора, есть диагональ квадрата со стороной 1. Если бы оно выражалось отношением натуральных чисел m и n, то отрезок длинной 1/n укладывался бы n раз в стороне единичного квадрата, и m раз в его диагонали, а значит, был бы их общей мерой, что невозможно.

Можно предположить и косвенное доказательство. Поскольку множества всех рациональных чисел четно, а множество всех действительных чисел нечетно, то должны существовать действительные числа, не являющиеся рациональными, то есть числа иррациональные.

Задача 18. Доказать, что для любого действительного числа a>0 и любого натурального N найдутся такие целые m≥0 и k>0, что ïka - mï≤ 1/N.

Доказательство. Разобьем отрезок [0, 1] точками 1/N, 2/N, …, (N-1)/N на N отрезков (рис. 3). Полученные отрезки будем считать “клетками”, а числа 1, 2, …, N+1 примем в качестве “зайцев”.

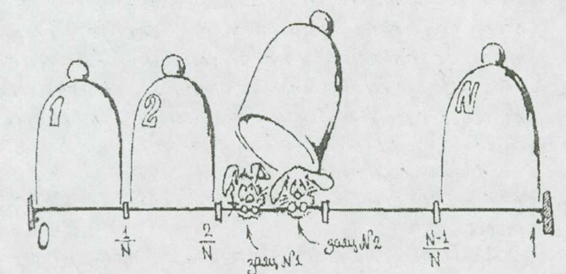
рис. 3

Если k – один из “зайцев”, то число ka можно записать в виде ka=m+x, где m – целое, 0≤ x ≤1 (то есть в виде суммы целой и дробной части). Число x попадает в одну из “клеток”, в эту “клетку” мы и посадим “зайца” k.

Так как “зайцев” больше, чем “клеток”, то найдутся два “зайца”, сидящих в одной “клетке”. Иначе говоря, среди чисел 1, 2, …, N+1 найдутся такие два числа k₁< k₂, что

k₁a = m₁ + x₁, 0≤ x₁<1,

k₂a = m₂ + x₂, 0≤ x₂<1,

причем x₁ и x₂ находятся в одной  “клетке”, и поэтому ïx₂ - x₁ï≤ 1/N.

Таким образом,

ï(k₂ – k₁)a - (m₂ – m₁)ï = ï(k₂a - m₂) - (k₁a - m₁)ï = ïx₂ – x₁ï≤ 1/N,

то есть числа k = k₂ – k₁ и m = m₂ – m₁, являются искомыми. Здесь k>0, так как k₂>k₁, и m≥0, так как k₂a - k₁a = (m₂ + x₂) – (m₁ + x₁) >0, откуда m₂ - m₁ > x₁ - x₂ > -1 (ведь 0≤ x₁<1 и  0≤ x₂<1), и поскольку m₁ и m₂ – целые числа, m₂ – m₁ ≥0.

Задача 19. В прямоугольнике 5×6 закрашено 19 клеток. Докажите, что в нем можно выбрать квадрат 2×2, в котором закрашено не менее трех клеток.

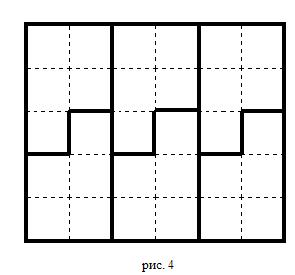 Доказательство. Разделим прямоугольник на 6 частей по 5 клеток (рис. 4). Согласно принципу Дирихле в одной из этих частей будет закрашено не менее 4 клеток. Тогда в квадрате 2×2, содержащимся в этой части, закрашено либо 3, либо 4 клетки. Это и будет искомый квадрат.

Задача 20. На длинной прямолинейной дороге с равными интервалами вырыты небольшие поперечные канавки (рис. 5). Расстояние между центрами каждых двух соседних канавок равно √2 метров. Доказать, что какими бы узенькими эти канавки ни были сделаны, человек, шагающий по дороге и имеющий длину шага 1 метр, рано или поздно попадет в одну из канавок. 

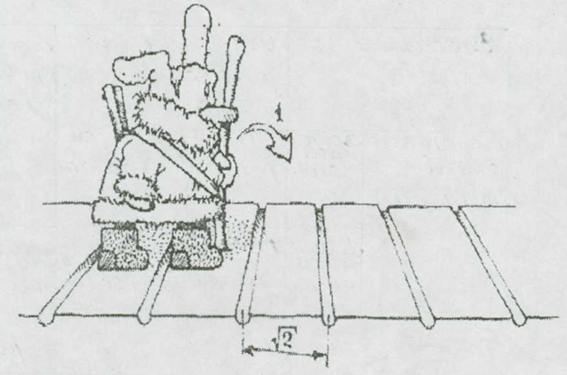
рис. 5

Доказательство. Представим, что мы можем “намотать” дорогу на барабан, длина окружности которого равна √2 метров. Тогда все канавки на этом барабане совместятся, а каждый шаг человека будет изображать на окружности дугой длины 1 метр. Будем последовательно отмечать на окружности след человека после первого, второго, третьего и так далее шагов. Нам надо доказать, что хотя бы один из этих следов попадет внутрь заданной на окружности дуги, изображающей канавку, какой бы малой ни была длина h этой дуги. Нетрудно понять, что если нам удастся найти такие k и m, для которых следы k-го и (k + m)-го шагов удалены друг от друга (на окружности) меньше чем на h, то требуемое утверждение докажется легко. Ведь еще после m шагов новый след (то есть (k + 2m)-й) опять сдвинется на расстояние меньшее h, затем мы рассмотрим следующие m шагов и так далее. Ясно теперь, что, сделав несколько раз по m шагов, мы неминуемо обнаружим след, попавший в канавку (потому что, перемещаясь на одно и то же расстояние, меньшее h, нельзя “перешагнуть” канавку ширины h). Итак, нужно найти два следа, находящиеся на окружности на расстоянии, меньшем h. Вот здесь-то и помогают “зайцы”. Действительно, разделим окружность на дуги, каждая из которых имеет длину меньше h; эти дуги мы и назовем “клетками”. Пусть их имеется p штук. Если мы возьмем число следов большее, чем p (заметим, что никакие два следа не совпадут в силу иррациональности числа √2), то по принципу Дирихле хотя бы в одну из клеток попадет более одного следа (“зайца”). Расстояние между двумя следами, попавшими в одну “клетку”, меньше h; этим наше утверждение и доказано.